Структурное моделирование
14.6. Структурное моделирование
При структурном моделировании моделируемая система, например, система автоматического управления задается в виде структурной схемы, в которую могут быть включены и отдельные ее реальные элементы (регуляторы, исполнительные органы и т.п.). В структурной схеме задаются параметры основных звеньев и указываются ориентировочные пределы изменения варьируемых параметров, например, коэффициентов усиления и постоянных времени звеньев. Моделирование каждого звена системы-оригинала осуществляется в отдельности, а затем из моделей звеньев составляется общая модель, точно воспроизводящая структурную схему оригинала.
Метод структурного моделирования имеет по сравнению с методом моделирования по уравнению то преимущество, что он позволяет включить в состав модели элементы реальной системы регулирования и легко подбирать параметры каждого звена модели, добиваясь желаемого закона регулирования. Кроме того, такой метод дает ясное представление о соответствии параметров исследуемой системы ее модели, что создает определенные удобства как при подборе параметров самих звеньев, так и корректирующих связей. Так как параметры каждого звена модели однозначно связаны с параметрами соответствующих звеньев реальной системы через постоянные масштабы, то полученные при моделировании результаты могут быть пересчитаны затем в параметры звеньев реальной системы, при которых достигается требуемый закон управления.
Для проведения структурного моделирования необходимо располагать моделями (схемами набора) элементарных звеньев систем управления. Рассмотрим такие модели, используя данные работ [63 — 65]. При составлении моделей будем придерживаться системы обозначений, принятых в [29] и использованных в разд. 14.1 и 14.4.
Апериодическое звено. Коэффициент передачи такого звена:
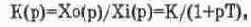
где Хо(р), Xi(p) — выходная и входная величины соответственно; К — коэффициент усиления звена; Т — постоянная времени звена; p=d/dt — оператор Лапласа.
Запишем выражение (14.27) в следующем виде:
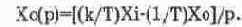
Введем масштаб по времени Мt тогда оператор Лапласа в формуле (14.28) заменяется на P-Mt и машинное уравнение модели может быть записано следующим образом:
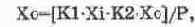
где
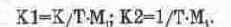
Выражение (14.29) позволяет нам достаточно наглядно проследить процесс формирования схемы набора. Действительно, из (14.29) видно, что он должен содержать интегратор, о чем говорит множитель 1/Р, при этом он должен одновременно выполнять и функции сумматора двух слагаемых (суммирующий интегратор). В таком случае модель в первом приближении может быть представлена в виде схемы на рис. 14.50, а. При выполнении условий
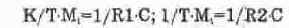
с учетом выражений (14.30) выходное напряжение схемы на рис. 14.50, а будет равно -Хо и, следовательно, выход можно соединить со вторым входом, поскольку они эквипотенциальны. Таким образом, окончательная схема набора для апериодического звена будет иметь вид на рис. 14. 50, б, а его коэффициент усиления, как видно из выражений (14.30) и (14.31), определяется формулой K=K1/K2=R2/R1.
Как видно из приведенного анализа, нами было использовано масштабирование только по времени. Объясняется это тем, что масштабирование вводится с целью обеспечения проведения моделирования в рамках технических возможностей компонентов модели. Это в первую очередь относится к возможным перегрузкам операционных усилителей по максимально допустимому выходному напряжению (например, в случае интеграторов). Однако такие ограничения устраняются не только за счет масштабирования по входному и выходному напряжению, но и за счет введения масштаба по времени. Кроме того, для избежания перегрузок ОУ вводят соответствующее распределение коэффициентов усиления по отдельным звеньям в каждой прямой (без обратной связи) ветви моделируемой системы.
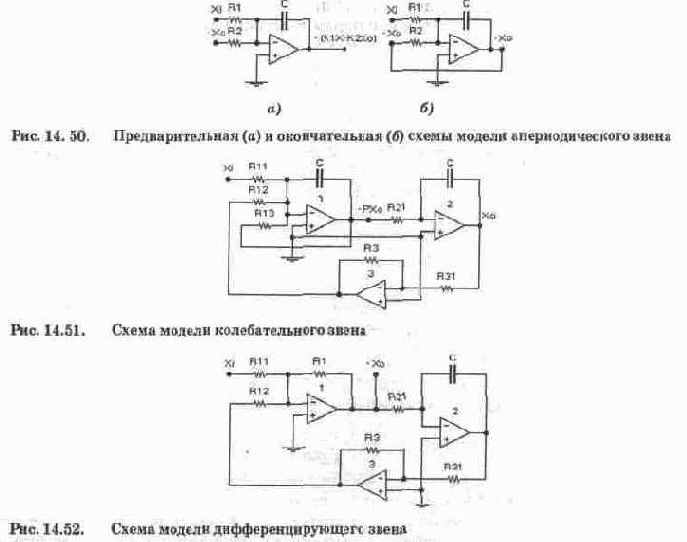
Колебательное звено [64]. Коэффициент передачи звена:
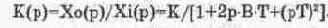
Модель звена показана на рис. 14.51. Она отличается от аналогичной модели на рис. 14.3 тем, что в ней совмещены функции сумматора и первого интегратора, что позволило уменьшить количество ОУ. Параметры компонентов модели определяются из следующих соотношений:
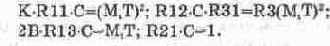
Дифференцирующее звено [64]. Коэффициент передачи звена:
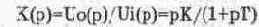
Модель звена показана на рис. 14.52. Параметры ее компонентов выбираются из соотношений:
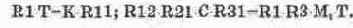
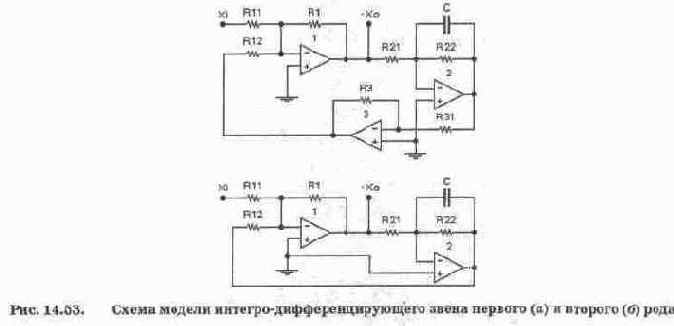
Интегоо-дифференцирующее звено Г641. Коэффициент передачи звена:
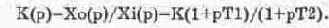
Для случая Т1>Т2 схема модели показана на рис. 14.53, а. Параметры ее компонентов определяются из соотношений:
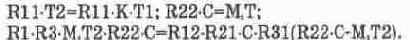
Для случая Т1<Т2 модель звена показана на рис. 14.53, б. Ее параметры выбираются из соотношений:
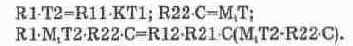
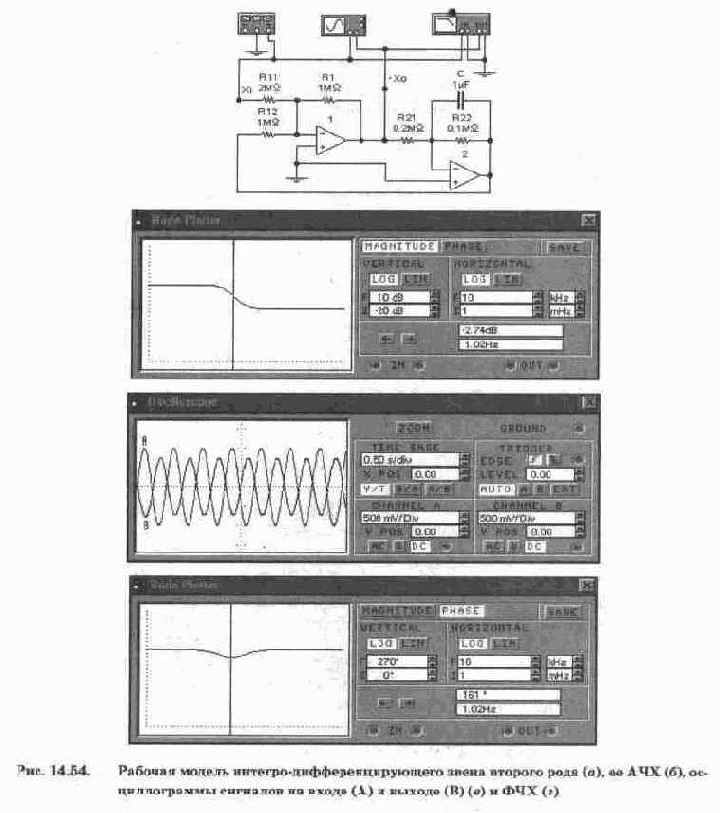
Проведём испытания модели на рис. 14.53, б при следующих исходных данных: Т1=0,1 с, Т2=0,2 с, К=1, R1=1 МОм, R12=1 МОм, М,=1. Из условий (14.38) получаем значения остальных параметров: R11=2 МОм, R22=0,1 МОм, R21=0,2 МОм. При таких данных модель с необходимыми контрольно-измерительными приборами показана на рис. 14.54, а. Результаты ее испытания приведены на рис. 14.54, б — АЧХ, на рис. 14.54, в — осциллограммы сигналов, на рис. 14.54, г — ФЧХ. Для проверки результатов испытаний проведем необходимые расчеты, используя формулу (14.34). После подстановки в эту формулу и несложных преобразований получим выражения для АЧХ и ФЧХ в следующем виде:
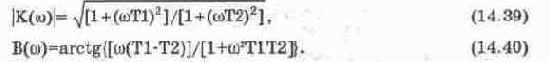
При расчетах используем принятые для схемы на рис. 14.54, а значения Т1=0,1 с, Т2=0,2 с и полученные в результате моделирования значение угловой частоты 6,41 рад/с (см. рис. 14.54, б и г). После подстановки этих значений параметров в формулы (14.39) и (14.40) получим 0,739=-2,63 дБ, -19,4°, что практически совпадает с результатами моделирования (относительно фазы заметим, что сигнал на выходе модели инверсный — см. обозначение -Хо на рис. 14.53, а — 14.54, а и осциллограммы на рис. 14.54, в).
Генератор постоянного напряжения с независимым возбуждением. Коэффициент передачи генератора определяется выражением:
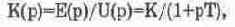
где Е(р) — ЭДС генератора; U(p) — напряжение на обмотке генератора; T=L/R — постоянная времени; L, R — индуктивность и активное сопротивление обмотки возбуждения; K=m/R — коэффициент передачи; m=E/I — крутизна линейной части характеристики холостого хода; Е — ЭДС генератора (в установившемся режиме); I — ток в обмотке возбуждения.
Из выражения (14.41) видно, что генератор постоянного напряжения с независимым возбуждением представляет собой апериодическое звено, т.е. в качестве его модели может быть использована схема на рис. 14.50, б. Для общего представле ния о порядке величин, входящих в выражение (14.41), приведем следующие данные [64]: m=08 В/А, R=65,5 Ом, L=27,5 Гн, К=1,65, Т=0,42 с.
Двигатель постоянного тока с независимым возбуждением. Передаточная характеристика двигателя по скорости определяется выражением [64]:
Из выражения (14.42) видно, что двигатель постоянного напряжения с независимым возбуждением представляет собой колебательное звено, т.е. в качестве его модели может быть использована схема на рис. 14.51.
Асинхронный двухфазный двигатель. Такой тип двигателя является наиболее распространенным (после двигателей постоянного тока) в системах управления. Его передаточный коэффициент без учета момента инерции нагрузки и внешнего скоростного трения определяется выражением:
Входящие в выражение (14.43) величины имеют такое же обозначение, что и в выражении (14.42).
С учетом нагрузки и внешнего трения (двигатель с редуктором) коэффициент передачи асинхронного двигателя определяется выражением:
Из выражений (14.43) и (14.44) видно, что асинхронный двигатель представляет собой апериодическое звено, т.е. в качестве его модели может быть использована схема на рис. 14.50, б.
Электромашинный усилитель с поперечным полем. Электромашинный усилитель (ЭМУ) представляет собой устройство, состоящее из генератора постоянного тока с одной или несколькими обмотками возбуждения (управления) и приводного двигателя. Приводной двигатель предназначен для вращения ротора генератора с некоторой постоянной скоростью и обычно представляет собой однофазный или трехфазный асинхронный нерегулируемый электродвигатель с корот-козамкнутым якорем. ЭМУ применяются в схемах следящего привода совместно с двигателями постоянного тока мощностью от нескольких десятков ватт до нескольких киловатт.
Статические и динамические свойства ЭМУ определяются совокупностью следующих характеристик:
Характеристика холостого хода — определяет зависимость выходной ЭДС ЭМУ от величины тока управления в установившемся режиме. Характеристика холостого хода является линейной функцией при условии, что магнитная система ЭМУ не насыщена.
Внешняя (нагрузочная) характеристика — определяет функциональную зависимость выходного напряжения от тока нагрузки в установившемся режиме.
Коэффициент усиления напряжения — определяется обычным образом и колеблется в пределах от нескольких единиц до нескольких десятков.
Коэффициент усиления мощности — пропорционален скорости вращения его якоря, колеблется в пределах от десятков до нескольких тысяч.
Добротность ЭМУ — характеризуется коэффициентом добротности, представляющим собой отношение коэффициента усиления по мощности к постоянной времени усилителя.
В зависимости от конструкции и способа возбуждения ЭМУ подразделяются на следующие типы:
1) с независимым возбуждением;
2) со смешанным возбуждением;
3) со специальной ориентацией магнитных потоков.
ЭМУ с независимым возбуждением представляет собой обычный генератор постоянного тока, обмотка возбуждения которого питается от регулируемого источника напряжения. Выходное напряжение ЭМУ с независимым возбуждением с достаточной степенью точности линейно зависит от скорости вращения его ротора. ЭМУ с независимым возбуждением дает возможность управлять значительными мощностями нагрузки при незначительных затратах мощности в обмотке управления. Коэффициент усиления по мощности для некоторых типов ЭМУ с независимым возбуждением может достигать значений 100 и более. Постоянная времени обмоток возбуждения обычно составляет десятые доли секунды.
ЭМУ со смешанным возбуждением представляет собой генератор постоянного тока, работающий в режиме самовозбуждения. ЭМУ со смешанным возбуждением отличаются от усилителей с независимым возбуждением тем, что необходимая для создания магнитного потока возбуждения мощность почти целиком поступает с выхода по цепи положительной обратной связи. Вследствие этого результирующий коэффициент усиления системы может быть достаточно большим.
Для третьего типа ЭМУ классификационными признаками являются число ступеней усиления и ориентация управляющего магнитного потока второй (и третьей) ступени усиления по отношению к управляющему магнитному потоку первой ступени усиления. По числу ступеней усиления ЭМУ подразделяются на одно-, двух-и трехступенчатые. По ориентации управляющего магнитного потока второй ступени двух- и трехступенчатые ЭМУ подразделяются на ЭМУ с поперечным, с продольным полем и с продольно-поперечным полем.
ЭМУ с поперечным полем представляет собой специальный генератор постоянного тока с якорем, выполненным по типу якорей обычных машин постоянного тока, но с дополнительной парой поперечных короткозамкнутых щеток (см. рис. 14.55). Благодаря такой конструкции ЭМУ с поперечным полем требует для возбуждения мощность, в десятки раз меньшую, чем соответствующая мощность возбуждения обычных генераторов. На статоре ЭМУ расположены одна или не- . сколько обмоток управления (на рис. 14.55 показана только одна обмотка Wy), обмотка дополнительных полюсов и компенсационная обмотка.
В ЭМУ с поперечным полем магнитный поток управления второй ступенью усиления расположен перпендикулярно к магнитному потоку управления первой ступенью. Так как принято считать, что магнитный поток первой ступени, создаваемый входной управляющей обмоткой, направлен по продольной оси ЭМУ (перпендикулярно рис. 14.55), то магнитный поток управления второй ступени направлен по поперечной оси ЭМУ. Поэтому этот класс двухступенчатых ЭМУ и получил название ЭМУ с поперечным полем.
При подаче на обмотку управления Wy сигнала управления в ЭМУ возникает продольный магнитный поток управления. В витках вращающегося с постоянной скоростью ротора (якоря) наводится ЭДС, при этом наибольшего значения она достигает в витках, расположенных в продольной плоскости ЭМУ. Напряжение этой ЭДС снимается поперечными щетками 1 (см. рис. 14.55). Поскольку они закорочены и сопротивление цепи мало, то в цепи протекает достаточно большой ток, что приводит к формированию значительного по величине поперечного магнитного потока. Этот процесс называется реакцией якоря по поперечной цепи (первая ступень усиления ЭМУ). Под действием усиленного таким образом магнитного потока в витках вращающегося якоря ЭМУ наводится ЭДС, максимальная величина которой имеет место в витках, расположенных в плоскости этого потока, т.е. в поперечной плоскости ЭМУ. Напряжение этой ЭДС, снимаемое продольными щетками 2, является выходным сигналом ЭМУ (вторая ступень усиления). Поскольку при подключенной нагрузке по поперечным виткам якоря ЭМУ протекает ток, то под действием этого тока в ЭМУ создается магнитный поток, направленный по продольной оси навстречу потоку. Это так называемая реакция якоря ЭМУ по продольной оси. Таким образом, в продольной оси ЭМУ будет действовать некоторый результирующий магнитный поток, который является функцией не только управляющего напряжения в обмотке Wy, но и параметров нагрузки. Для уменьшения противодействующего магнитного потока в статоре ЭМУ используется компенсационная обмотка, с помощью которой достигается компенсация продольной реакции якоря.
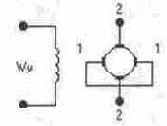
Рис. 14.55. Упрощенная схема ЭМУ с поперечным полем
Динамика работы ЭМУ описывается достаточно сложными и громоздкими выражениями [65]. На практике же при проведении расчетов систем управления используются упрощенные выражения. Для коэффициента передачи двухкаскадного ЭМУ с поперечным полем оно имеет следующий вид:
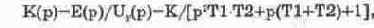
где Е(р), Uy(p) — ЭДС якоря по продольной оси и напряжение на управляющей обмотке; K=NyMe/Ry —коэффициент усиления ЭМУ по напряжению; Ny — число витков управляющей обмотки (3200); Мe — угловой коэффициент холостого хода ЭМУ, определяемый отношением ЭДС якоря по продольной оси к магнитодвижущей силе, создаваемой обмоткой управления (4,2 В/А-В); Ry — активное сопротивление обмотки управления (2 кОм); Tl=Ly/Ry — постоянная времени обмотки управления; Ly — индуктивность обмотки управления (80 Гн); T2=Lq/Rq — постоянная времени поперечной цепи якоря ЭМУ; Lq, Rq — индуктивность (0,16 Гн) и активное сопротивление (1,23 Ом) поперечной цепи якоря.
Из выражения (14.45) видно, что ЭМУ с поперечным полем представляет собой колебательное звено, т.е. в качестве его модели может быть использована схема на рис. 14.51.
Дифференцирующий трансформатор используется в системах управления в качестве согласующего и корректирующего элемента. Его схема приведена на рис. 14.56, на котором буквой М обозначен коэффициент взаимной индуктивности обмоток. Типичные значения параметров трансформатора [64]: число витков, индуктивность и активное сопротивление обмоток N1=420, L1=l,15 Гн, R1=24 Ом — для первичной и М2=2680, L2=47 Гн, Р2=2200 Ом — для вторичной; индуктивность и сопротивление нагрузки Lн=110 Гн, Rн=2200 Ом.
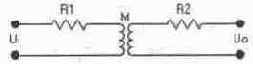
Рис. 14.56. Схема дифференцирующего трансформатора
При работе на индуктивную нагрузку (например ЭМУ) коэффициент передачи трансформатора определяется выражением:
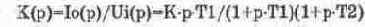
где Io(p), Ui(p) — ток вторичной и напряжение первичной обмоток, K=n/Ro, n=N2/N1 — коэффициент трансформации, Ro=R2+Rн — суммарное сопротивление вторичной обмотки и нагрузки, Tl=L1/(R1+R1) — постоянная времени первичной обмотки, R, — внутреннее сопротивление источника входного сигнала, T2=(L2+Lн)/Ro — постоянная времени вторичной обмотки.
Из выражения видно, что в качестве модели дифференцирующего трансформатора могут быть использованы последовательно включенные модели дифференцирующего и апериодического звена.
Если трансформатор работает на высокоомную нагрузку (например, усилитель с высоким входным сопротивлением), то постоянной времени Т2 в формуле (14.46) можно пренебречь и в этом случае дифференцирующий трансформатор может моделироваться дифференцирующим звеном.
Тахогенератор является электромеханическим преобразователем скорости вращения в электрический сигнал постоянного или переменного тока. По существу это обычные электрические генераторы малой мощности. Коэффициент передачи тахогенератора постоянного тока определяется выражением [65]:
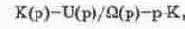
Как видно из выражения (14.47), тахометр является идеальным дифференцирующим звеном.
Сельсины. Индукционная синхронная передача на сельсинах в простейшем случае состоит из двух электрически связанных между собой сельсинов одинаковой конструкции. Сельсин как элемент синхронной передачи представляет собой электрическую машину переменного тока с однофазной обмоткой возбуждения и трехфазной обмоткой синхронизации.
В зависимости от выполняемых функций в схемах синхронной передачи угла и вращения сельсины разделяются на сельсины-датчики, сельсины-приемники, дифференциальные сельсины-датчики и приемники, сельсины-трансформаторы. Сельсин-датчик используется в качестве элемента, воспроизводящего угловые перемещения командного вала и передающего их сельсину-приемнику. Сельсин-приемник воспроизводит закон движения, заданный сельсином-датчиком, в виде углового перемещения ротора, пропорционального угловому перемещению ротора сельсина-датчика. С помощью дифференциального сельсина-датчика (или приемника) производится алгебраическое суммирование величин угловых перемещений. Сельсин-трансформатор воспроизводит закон движения, заданный сельсином-датчиком, в виде электрического напряжения, пропорционального угловым перемещениям ротора сельсина-датчика.
В системах автоматического регулирования сельсины обычно используются в двух основных режимах работы индукционных синхроннных передач: индикаторном и трансформаторном (измерительном).
При индикаторной синхронной передаче обмотку синхронизации сельсина-датчика соединяют с обмоткой синхронизации сельсина-приемника. На обмотки возбуждения сельсинов подается напряжение питания. Если угловые положения роторов датчика и приемника неодинаковы, то под действием возникающих синхронизирующих моментов они приходят в согласованное положение. При принудительном вращении ротора сельсина-датчика вал ротора сельсина-приемника вращается с той же скоростью, что и вал ротора датчика, т.е. следит за угловым положением ротора датчика.
При трансформаторной (измерительной) синхронной передаче обмотку синхронизации сельсина-датчика соединяют с обмоткой синхронизации сельсина-трансформатора. Обмотку возбуждения сельсина-трансформатора включают на нагрузку. Напряжение питания подается на обмотку возбуждения сельсина-датчика. При повороте ротора датчика на некоторый угол в однофазной обмотке сельсина-трансформатора наводится ЭДС, амплитуда которой пропорциональна углу рассогласования между угловыми положениями роторов сельсина-датчика и сельсина-трансформатора, а фаза зависит от направления или знака рассогласования.
Основными характеристиками сельсинов являются: статический и динамический синхронизирующие моменты, крутизна кривой статического синхронизирующего момента, точность синхронной передачи, влияние скорости и ускорения на погрешности схемы, коэффициент добротности, устойчивость положения осей системы, влияние колебаний напряжения, частоты питающей сети и длины соединительной линии на погрешность системы, влияние количества приемников, работающих одновременно от одного датчика.
Основной характеристикой дистанционной передачи является зависимость статического синхронизирующего момента от угла рассогласования между роторами датчика и приемника в положении покоя (все характеристики передачи обычно определяют по отношению к приемнику, поскольку роторы сельсинов-датчиков перемещаются принудительно).
Крутизна кривой статического синхронизирующего момента определяет удельный синхронизирующий момент, развиваемый на валу приемника при его рассогласовании с датчиком на один градус.
Динамический синхронизирующий момент — это момент, развиваемый системой на валу приемника в режиме вращения.
Статическая точность передачи характеризуется величиной статической ошибки, определяемой углом рассогласования между осями датчика и приемника в состоянии равновесия (при отсутствии вращения). Величина статической ошибки зависит от нагрузки или внешнего момента на валу приемника, а также от собственной погрешности сельсинов. В зависимости от величины собственной погрешности сельсины различают по классам точности (от 0,25' до 1° для датчиков и от 0,75° до 2,5° для приемников). Величина, обратная статической ошибке, характеризует добротность синхронной передачи.
Динамическая точность характеризуется величиной динамической ошибки, определяемой углом рассогласования между осями сельсина-датчика и сельсина-приемника в режиме вращения. Динамические ошибки также измеряются в градусах.
Устойчивость положения осей системы в положении равновесия характеризует способность роторов сельсинов-приемников сохранять неизменным заданное положение при внешних воздействиях.
Динамика сельсинной передачи в большинстве практических случаев может быть описана системой первого порядка, т.е. в качестве ее модели может быть использована модель апериодического звена.
Вращающийся трансформатор (ВТ) представляет собой устройство, в конструктивном отношении имеющее много общего с асинхронной машиной с неявно выраженными полюсами. Принцип действия ВТ основан на использовании его свойства изменять взаимоиндуктивность между обмотками статора и ротора (при повороте последнего) по закону, близкому к синусоидальному. На статоре и роторе ВТ обычно размещаются по две распределенные обмотки, магнитные оси которых взаимно перпендикулярны. Ротор поворачиваться относительно статора на некоторый произвольный угол, максимальная величина которого зависит от конструкции ВТ.
Одна из обмоток ВТ (обычно статорная) питается однофазным переменным током и называется первичной обмоткой, или обмоткой возбуждения. Схема включения остальных обмоток определяется заданной зависимостью, воспроизводимой с помощью ВТ. Выходная величина, пропорциональная воспроизводимой функции, снимается в виде электрического напряжения переменного тока со вторичной обмотки. Вторичная обмотка обычно располагается на роторе.
ВТ в различных модификациях применяются в качестве функциональных преобразователей, а также как чувствительные элементы, фиксирующие отклонение системы от некоторого определенного положения.
По характеру токосъема ВТ делятся на контактные и бесконтактные. Контактные ВТ конструируются таким образом, что токосъем с обмотки ротора может быть осуществлен либо с помощью колец и щеток, либо с помощью спиральных пружин. В последнем случае угол поворота ротора ограничивается максимальным углом закручивания спиральных пружин. Токосъем в конструкциях бесконтактных ВТ осуществляется за счет использования индуктивной связи статорных и роторных цепей.
Параметры ВТ определяются сопротивлением холостого хода, коэффициентом трансформации и материалом магнитопровода.
Сопротивление холостого хода измеряется на рабочей частоте при разомкнутой вторичной цепи. Численные значения сопротивления холостого хода ВТ колеблются в пределах 250...4500 ом.
Коэффициент трансформации определяется отношением максимального вторичного напряжения к напряжению возбуждения. Численные значения коэффициентов трансформации отдельных образцов ВТ могут изменяться в пределах от 0,1 до 1,0.
В качестве материала магнитопроводов ВТ применяется железо или пермал-лой. Магнитопровод из железа обычно используется в тех случаях, когда ВТ работает непосредственно от сети или иного мощного источника питания; в многокаскадной схеме или при работе от маломощного источника питания, как правило, используют вращающиеся трансформаторы с магнитопроводом из пермаллоя.
Точность ВТ определяется максимальной погрешностью воспроизведения заданной функции. В зависимости от величины этой погрешности вращающиеся трансформаторы делятся на группы, соответствующие трем классам точности: первый класс — с погрешностью до 0,1%; второй класс — от 0,1 до 0,25%; третий класс — более 0,25%
В качестве модели ВТ может быть использована модель дифференцирующего или апериодического звена.
Таким образом, в большинстве случаев элементы систем автоматического регулирования могут быть представлены в виде рассмотренных в начале раздела четырех типов звеньев.
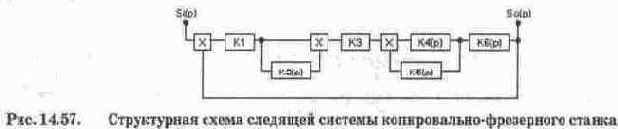
Перейдем теперь к структурному моделированию систем управления. В качестве примера рассмотрим процесс моделирования следящей системы копировально-фрезерного станка [64], структурная схема которой показана на рис. 14.57. Для этой системы необходимо провести исследование переходных процессов при входном воздействии Si(p)=l. В состав системы входят (см. рис. 14.57) преобразующее устройство с коэффициентом передачи К1=10 В/мм; дифференцирующий трансформатор с коэффициентом передачи К2(р)=рК2/(1+рТ2), где К2=0,104 с, Т2=0,0303 с (схема модели на рис. 14.52); электронный усилитель с коэффициентом передачи К3=6,3;
ЭМУ с коэффициентом передачи К4(р)=К4/(1+рТ4), где К4=35,6, Т4=0,0616 с — постоянная времени поперечной цепи якоря (схема модели на рис. 14.50, б); звено обратной связи по скорости с коэффициентом передачи К5(р)=рК5/(1+рТ5), где К5=0,027 с, Т5=0,134 с — электромеханическая постоянная двигателя (схема модели на рис. 14.52); электродвигатель с редуктором с коэффициентом передачи К6(р)=рК6/(1+рТ5), где К6=0,053 мм/В-с — передаточный коэффициент электродвигателя по скорости (схема модели состоит из последовательно включенных модели апериодического звена и интегратора); масштаб по времени Mt=20. Дополнительным условием является введение ограничения на коэффициент усиления ОУ с ООС — не более 10 (такие ограничения характерны для реальных моделирующих установок).
Рабочая модель (схема набора) рассматриваемой системы показана на рис. 14.58. Входное единичное воздействие в схеме модели имитируется источником постоянного напряжения Ui=l В, преобразующее устройство — сумматором на ОУ 1, дифференцирующий трансформатор — дифференцирующим звеном на ОУ 2, 3 и 4 (см. рис. 14.52), электронный усилитель — сумматором на ОУ 5, ЭМУ — апериодическим звеном на ОУ 6 (см. рис. 14.50, б), звено гибкой обратной связи — дифференцирующим звеном на ОУ 7, 8 и 9 (см. рис. 14.52), электродвигатель с редуктором — апериодическим звеном на ОУ 10 и интегратором на ОУ 11. Таким образом, модель составлена в соответствии со структурной схемой из моделей типовых звеньев.
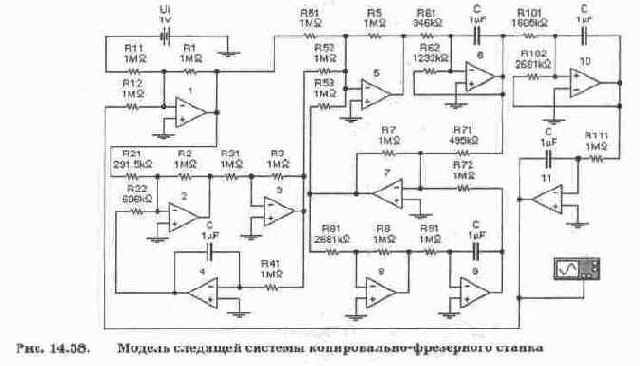
Проведем предварительный выбор передаточных коэффициентов каждого компонента модели, отмечая их штрихом и следуя методике, изложенной в [64], и системе обозначений, принятой в [29]. Для преобразовательного звена задаемся K11'=R1/R12=1, K12'=R1/R12=1 (коэффициент передачи звена К1 будет учтен при выборе параметров интегратора на ОУ 11). Для дифференцирующего трансформатора задаемся КЗ1'=1, на основании (14.35) находим K21'=R2/R21=K2/T2= =0,104/0,0303=3,43, K22'.K41'=(R2/R22)(l/R41-C)=l/MtT2=l/20-0,0303=l,65, откуда, задавшись K41'=1/R41-C=1, получим K22'=R2/R22=1,65. Для сумматора на ОУ 5 задаемся K51'=R5/R51=1, K52'=R5/R52=1, K53'=R5/R53=1 (коэффициент усиления звена КЗ будет учтен при выборе параметров интегратора на ОУ 11). Для ЭМУ на основании (14.31) рассчитываем К61'=1/Р61-С=К4/МtТ4= =35,6/20-0,0616=28,9, K62'=1/R62-C=1/M..T4=1/20-0,0616=0,812. Для элемента обратной связи по скорости на основании (14.34) рассчитываем K71'=R7/R71= =К5/Т5=0,027/0,134=0,202, K72'-K81'.K91'=(R7/R72)(R8/R81)(1/R91.C)=1/M,.T5= =1/20-0,134=0,373, откуда, задавшись K72'=(R7/R72)=1, K91'=1/R91-C=1, получим K81'=R8/R81=0,373. Поскольку электродвигатель с редуктором представлен апериодическим звеном на ОУ 10 и интегратором на ОУ 11, то его коэффициент передачи К6=0,053 разобьем на два: 1 — для апериодического звена и 0,053 — для интегратора. В таком случае для апериодического звена на ОУ 10 на основании (14.31) получаем К101'=1/Р101-С=1/М,-Т5=1/20.0,134=0,373, К102'=1/К102-С=1/М».Т5= =1/20-0,134=0,373. Для интегратора на ОУ 11с учетом принятых выше условий коэффициент передачи K111'=1/R111-С=К1.КЗ-К6/М.=10-6,3(0,053)/20=0,167.
Поскольку коэффициент передачи К61' получился больше оговоренного в условиях задачи, то уменьшим его в 10 раз, при этом для сохранения прежнего значения петлевого усиления (в петле обратной связи) необходимо увеличить в 10 раз коэффициент передачи К7Г. Кроме того, для сохранения произведения К1-КЗ-К4-К6 необходимо увеличить в 10 раз и значение коэффициента Kill'. Последнее изменение связано с обеспечением удобства набора на реальной моделирующей установке — выбираем коэффициент передачи К111'=1, при этом коэффициент К10Г необходимо увеличить в 1.67 раза. После внесения указанных изменений коэффициенты передачи модели на рис. 14.57 принимают следующие окончательные значения, на основании которых и были выбраны параметры ее компонентов:

Результаты моделирования рассматриваемой системы при входном воздействии в виде единичного потенциального скачка представлены на рис. 14.59, а осциллограммами переходного процесса. Длительность переходного процесса с учетом принятого масштаба составляет (см. результаты измерения в индикаторных окнах на рис. 14.59, а) Т2/М,=10,08/20=0,5 с, количество колебаний — 1, что полностью совпадает с результатами расчета и моделирования на моделирующей установке МН-7, полученными в работе [64]. Величина перерегулирования, как видно из строки VA1 индикаторного окна, составляет около 0,42 В, т.е. 42%, что на 8% меньше полученного в [64]. Результаты осциллографических измерений дополним фазовой траекторией модели, показанной на рис. 14.59, б. Как показали измерения, время от начала моделирования до прихода изображающей точки к установившемуся значению выходной величины соответствует времени переходного процесса. Кроме того, с помощью фазовой траектории можно определить (см. рис. 14.59, б) величину перерегулирования и число колебаний.
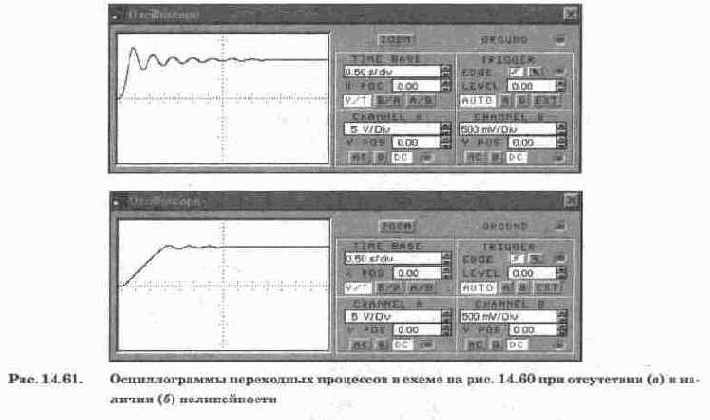
Схема на рис. 14.58 может быть использована также для исследования нели-нейностей в автоматических системах. Ее схема для такого применения показана на рис. 14.60. В ней изменены коэффициенты передачи К21, К62, К81, К101, К102 и Kill, что позволило повысить колебательность и уменьшить масштаб времени для обеспечения возможности наблюдения переходного процесса при ограниченной длительности развертки (1 с/дел). Схема модели дополнена переключателем Z, с помощью которого в цепь обратной связи ОУ 1 можно включить ограничительную цепь из параллельно включенных диодов VD1, VD2 и тем самым имитировать нелинейность типа насыщения ОУ (ограничения по координатам).
Осциллограмма переходных процессов при входном воздействии в виде потенциального скачка в 10 В (Ui = 10 В) в положении ключа Z, показанном на рис. 14.60 (цепь ограничения отключена), приведена на рис. 14.61, а, а при замкнутом ключе Z (цепь ограничения включена) — на рис. 14.61, б. Из сравнения осциллограмм на рис. 14.61 видно, что введение нелинейности в систему управления существенно влияет на переходные процессы — уменьшается перерегулирование, сокращается время переходных процессов и уменьшается колебательность (увеличивается демпфирование).

Контрольные вопросы и задания
1. Используя условия (14.37) и схему на рис. 14.53, а, составьте рабочую модель интегро- дифференцирующего звена первого рода, проведите ее испытание путем сравнения результатов моделирования с результатами расчетов по формулам (14.38) и (14.39).
2. Как следует из выражения (13.34), схему модели дифференцирующего звена можно было составить из последовательно включенных дифференциатора и апериодического звена. Почему авторы работы [64] не пошли по такому пути?
3. Используя формулы (14.27) и (14.31) — (14.35), составьте выражения для АЧХ, ФЧХ и рабочие модели апериодического, колебательного и дифференцирующего звеньев. Проведите испытания этих моделей путем сопоставления результатов моделирования с результатами расчета по полученным формулам для АЧХ и ФЧХ (по аналогии с рассмотренным процессом испытания модели на рис. 14.54, а).
4. Каким образом можно моделировать генератор и двигатель постоянного тока?
5. Приведите схему модели асинхронного двигателя переменного тока.
6. Как устроен ЭМУ с поперечным полем? Можно ли использовать электродвигатель постоянного тока в качестве ЭМУ?
7. Для каких целей используются сельсины и вращающиеся трансформаторы?
8. Назовите основные характеристики сельсинов и вращающихся трансформаторов.
9. Для каких целей используются дифференцирующие трансформаторы? Назовите элементы схемы на рис. 14.58, имитирующие дифференцирующий трансформатор.
10. Проведите расчеты переходного процесса следящей системы на рис. 14.57, если известно, что при единичном входном сигнале ее выходное напряжение определяется выражением [64]: So(t)=l+l,12exp(-14,75t)+2,llexp(-7,6t)-cos(12,9t+3,37)--0,025exp(-143t). Результате расчета сравните с результатами моделирования.
11. В какую точку схемы на рис. 14.58 необходимо подключить вход канала В осциллографа, чтобы получить фазовую траекторию на рис. 14.59, б.
12. Отключите в модели на рис. 14.58 элементы, имитирующие дифференцирующий трансформатор, и проведите моделирование. Полученные результаты сравните с результатами на рис. 14.59.
13. В модели на рис. 14.58 отключите элементы, имитирующие цепь обратной связи по скорости, и проведите моделирование. Полученные результаты сравните с результатами на рис. 14.59.
14. Исследуйте зависимость перерегулирования, времени переходных процесов и колебательности (числа колебаний за время переходных процессов) от входного сигнала (воздействия) Ui в диапазоне от 0,5 до 15 В в модели на рис. 14.60. Используйте для этой цели как осциллограммы переходных процессов, так и фазовые траектории.